Miniature Ball Bearings in Clocks by Rex Swensen - Sydney
Part 1 - The Case for Miniature Ball Bearings in Clocks

Introduction
The traditional clockmaker usually frowns at the suggestion that ball bearings may be used in clocks, but even the famous English clockmaker, John Harrison, attempted to make a caged ball bearing and did make anti-friction wheels. However, in his quest to miniaturize the chronometer, he replaced this early use of anti-friction wheels with tiny jewelled journal bearings.
I am sure that if miniature bearings of the quality and price of today had been available in Harrison’s time, he would have jumped at them with glee!
Many amateur clockmakers of today do use ball bearings for the great wheel arbor, or if month going, also the intermediate arbor, since these are all heavily loaded. But what about the higher order arbors right up to the escape wheel arbor, or even the pallet arbor?
Figure 1 shows a bearing that has a bore of 0.6 mm and OD of 2.0 mm – now that is tiny! This bearing was announced by Dynaroll in the USA in 2004.

Again, the traditionalist will say that a highly polished small diameter pivot of hardened steel, running in a well burnished hole, or better still, in an olive jewelled bearing, and well lubricated, cannot be beaten. In this paper I will atteraces available today are quite economical and win significantly on reduced friction, probably longer life and lower maintenance. Being a retired mechanical engineer I had always been interested in this question, so my research into the matter was triggered by the discovery that Erwin Sattler in Munich, the eminent modern day maker of high quality mechanical clocks, had moved extensively to the use of tiny ball races in their clock trains as shown in one of their photos, Figure 2. Here there is a ball race on every rotating arbor. But my curiosity was to determine, if possible, how much better ball bearings would be, particularly in the upper reaches of the train, and what was the “down side”. In fact, should they be used on all arbors? The smallest bearings under consideration here have an ID of 2mm and OD of 5mm, being a popular and relatively inexpensive size.
Evaluation Criteria
The major factors to be considered are:
Friction – coefficient of friction
Lubrication
Corrosion
Bearing Life and Future Availability
Service
Robustness
Cost
Coefficient of Friction
To me, this is the major criteria. Throughout this investigation, the C of F, commonly referred to as Mu or µ, will be expressed in terms of the equivalent journal diameter, as if it were a plain pivot of 1.0 mm diameter. So even if a 2mm bore ball race is compared to a 1mm diameter plain pivot, the µ will be calculated at the effective diameter of 1mm. (see Appendix for definition of µ).
The challenge was to obtain numerical results for a variety of bearings, considering the stop–start nature of the clock train mechanism.
It is well known that the static µ for normal sliding friction is higher than dynamic friction, and this is true for ball races also, according to bearing manufacturers. It is also recognised that ball races are at their best when loads and speeds are relatively high, neither of which apply in a clock. In spite of these apparent disadvantages, the challenge was to actually measure µ for ball bearings in a “clock like” environment and see how they compared with traditional pivots.
Methodology

>It was felt that a short swinging pendulum, with the pivot provided by the bearing under test, would provide a simple and easily constructed test rig, provided that the amplitude was kept small. In this way the predominant damping force would be the friction in the bearing, and not air friction on the pendulum bob. This type of damping is known as Coulomb damping, and should result in a constant rate of decay. It would also provide a combination of static and dynamic friction similar to that found in the stop-start nature of a clock. The assumption of linear decay would also be verified if possible. The test pendulum has a length of 111 mm.
To compute the value of µ, the amount of potential energy in the little pendulum at the start of the oscillation is dissipated by frictional drag entirely over the successive oscillations of the pendulum until it comes to a stop. A simple equation may be derived from this relationship. It works out to be:
μ< = 90 L(1- cos(α))/ (N. r. π. α) Equation 1
Where :
μ = Coefficient of friction
L = Pendulum effective length mm (111 mm)
α = Initial pendulum amplitude angle º
r = Effective pivot radius mm (0.5 mm)
N = Observed number of full oscillations for decay
See Appendix for the derivation of this equation.
Shortly after my research was commenced some years ago, Dr Richard Stephen published results of similar experiments using a similar methodology in HJ November 2005. These results will be referred to later in this article.
Test Rigs

Two test rigs are shown in Figures 3 and 4. Preliminary tests were conducted in the single bearing rig while more serious tests were made in the double bearing rig. Here the bearings under test were inserted into the ends of the bearing tube which is then held in the lathe drill chuck for convenience. The mini pendulum hangs from the middle of a small arbor which is pivoted in the test bearings. A clearance cut-out ensures that the pendulum rod does not foul the supporting tube. The angle bracket on the lathe cross slide as shown in Figure 3 has a line inscribed to show bottom dead centre. The cross slide was used to accurately move the datum for the requisite starting amplitude for each test. The mass of the bob approximates the typical bearing load for an upper arbor. When plain pivots were under test, bearing inserts were made for the tupivot steel. Some preliminary tests were conducted with the mini pendulum hanging on a single ball race as shown in Figure 3, and these worked as well as the twin bearing rig shown above.
The coefficient of friction was computed by equating friction in the bearing. Hence the effective coefficient of friction µ,could easily be calculated using the equation shown above. It is important to note that this calculation was performed as if the pivot diameter was 1 mm even though most of the bearings had an ID of 2 mm. For great wheel bearings, with an ID of 5 mm, the equivalent pivot was calculated as if it were 5 mm in diameter.
An Excel spreadsheet was used to store results and perform all calculations. The pendulum was started at the desired amplitude and the number of cycles were either counted until the oscillations ceased, or the time measured by stop watch and the cycles computed which was necessary with the ball races.
Checking for Coulomb Damping
It would have been desirable to record the actual decay, cycle by cycle, but this was beyond my instrumentation capability. However, some approximation of the decay envelope could be achieved by starting the oscillation from a variety of initial deflections and overlaying the results in the Excel graph, as shown in Figure 5. Theoretically, for Coulomb damping, this should be a straight line showing linear decay as in the red line. The actual results confirm that Coulomb damping is a reasonable assumption. The mini pendulum has a full double swing cycle period of 0.68 seconds, i.e. it is a 0.34 seconds pendulum in normal clock maker parlance.

Ball Bearings Under Test
The ball bearings tested were procured in Australia from Miniature Bearings Australia via their web site: (www.smallparts.com.au). They are all shielded to exclude dust. Note that there is no contact between the shield and the inner race since it is a labyrinth seal. It is interesting that Sattler use open races. A bearing with 2mm bore was chosen for the main testing since it is small enough for upper arbors, yet has a reasonable price. Note that sealed bearings should NOT be used since the flexible seals usually make positive contact with the inner race, hence much higher friction.
Bearings tested are shown in Figure 6:

• 2 x 5 x 2.3mm (Bore, OD, Width) economy chrome steel - suitable for higher arbors
• 2 x 5 x 2.3mm higher quality stainless steel. - suitable for higher arbors
• 5 x 11 x 5mm economy chrome steel - suitable for great wheel arbors and weight pulleys
• Plain 1mm traditional pivot as used in higher arbors – polished pivot steel in brass hole
• Jewel bearings 1 x 2.6 x .5mm with chamfered oil sink in one side with polished pivot steel.
It was expected that the lubrication in the ball bearings, as received, would have a significant effect on results, and this proved to be the case. Tests were conducted “as received”, then after soaking in kerosene (paraffin) and isopropyl alcohol. I later discovered that white spirit is a far better solvent. It is known that a completely dry bearing would yield the lowest µ and this is recommended by bearing makers for applications where minimum friction is required. However potential life may be somewhat reduced.
Friction Test Results
The bearing prices listed below were as procured in 2004, and in all cases bulk purchases for the Sydney Clockmakers Society ensured very good prices. Since then all bearings, especially the stainless steel variety, have risen sharply in price.
1) Economy 2mm Bearing - Safe static load 5.0 Kg. Price ~ $A0.85 (2004 price)
This bearing received the most detailed initial testing.
Starting Amplitude - deg 1.500 1.125 0.750 0.375
Calculated µ as received 0.0053 0.0044 0.0052 0.0062
Calculated µ after soaking in solvent 0.0023
Ten of these bearings were purchased in a packet, and four were tested with the 1.125 deg swing. Results were substantially the same and were within the realm of experimental error.
2) Stainless Steel 2mm Bearing - Safe static load 5.0 Kg. Price ~$A1.85 (2004 price)
Tested in the twin bearing rig shown in Figure 4. This was the main test.
Starting Amplitude – deg 1.1250
Calculated µ as received 0.0190
Calculated µ after solvent soaking 0.0026 (isopropyl alcohol)
3) Economy 5mm Bearing - Safe static load 26.0 Kg.
This bearing was packed with grease, and fairly stiff, so it was well soaked in kerosene before testing.
Starting Amplitude – deg 1.125
Calculated µ after soaking 0.0078
Note that the safe static loads shown for all ball races above are as quoted by Dynaroll in the USA. A further factor of safety of five or more is recommended for clock mechanisms.
4) Plain 1mm Pivot – polished pivot steel in brass hole
This proved to be the most difficult to test on the pendulum rig. With such small starting amplitudes, the decay appeared to go through two distinct phases. Initially rapid decay, presumably while the rotating friction was in effect, then an extremely long period of very slow decay commencing at a very small amplitude. This latter phase was thought to be when the pivot was rolling within the radial clearance of the bearing hole, almost like a radiused knife edge. The total decay times were therefore quite meaningless.
An attempt was made to measure the number of cycles for the decay to reach the half amplitude point, presumably while sliding friction was still in control. This gave a µ of 0.16 dry and 0.22 lubricated, which seemed rather odd. Perhaps the drag effect of the lubricant, which was normal clock oil, accounts for the strangely higher µ for the oiled results.
I therefore think it is safe to assume that the effective µ for a hardened and polished steel pivot in brass, lubricated with clock oil, will be about 0.20 considering that the effect of combined static and dynamic friction is present.
5) Jewelled Pivots
A pair of 1.00 mm bore ruby jewels, with a deep oil sink on one side, were mounted in bearing bushings in the test rig similar to Figure 4 and tested. Two sequences were tested with two different diametric clearances, both dry and lubricated. To eliminate the rolling contact problem found with plain pivots as shown above, the half amplitude decay approach was again used. The starting amplitude was 3 deg with finishing amplitude 1.5 deg, so the decay was measured over 1.5 deg.
Test results:
Diametric clearance 0.04 mm 0.08 mm
Dry µ = 0.17 µ = 0.17
Oiled µ = 0.18 µ = 0.18
Surprisingly the results were the same for both diametric clearances. Again the oiled result came out slightly higher than the dry. According to a supplier of these jewels in the USA, a µ value of 0.15 is quoted, although I have seen values as low as .1 on other Internet sites. So the friction effects for jewelled bearings are not significantly lower than plain pivots.
It should be noted that the accuracy of the plain pivot tests is based upon the counting of cycles and observing when the amplitude reaches the half amplitude mark. This is rather difficult to do on such a rapidly oscillating pendulum so the precision is about 1 in 16 cycles and the µ value is rounded to two significant digits.
The big advantage of jewels appears to be in their wear resistance, and hence a much longer life than plain brass pivot holes. Also one may feel that they look more impressive in a clock and have popular “sales appeal”.
6) Anti-Friction Wheels
At a meeting of the Sydney Clockmakers Society, one of the members showed an “anti-friction wheel” which he had made. It was a finely crossed out wheel some 55mm in diameter made from .63 mm brass. The concept here provides two of these wheels to support and contain each pivot on their rim as a rolling contact bearing, with each anti-friction wheel running on a jewelled arbor. If the pivot in question was say 1.5 mm diameter, the effective µ for the anti-friction pivot “bearing” would be approximately .15 x (1.5/55) = 0.004 which is similar to that of a ball race. This is the type of bearing that Harrison used on some of his early H clocks. However the complexity of wheels andarbors becomes quite daunting. This type of bearing may be seen in a clock made by a professional clockmaker who had recently immigrated to Australia from England. He operates under the name of Buchanan of Chelmsford. The clock in question, is shown on the cover of the April 2006 edition of the Horological Journal, which also describes this clock in detail. The clock is a truly magnificent achievement. Another clock under construction by this maker is shown on the covers of the January 2010 HJ. It too has anti-friction wheels in addition to ball races.
I understand that he is now mounting his antifriction wheels on ball races so the equivalent µ would be approximately 0.003 x (1.5/55) = .00008! Virtually no friction at all!
Pivot Friction Research by Dr Richard Stephen – HJ September 2005

Subsequent to my studies, Dr Richard Stephen conducted similar experiments and reported them in the HJ. Dick had access to much more elaborate electronic test equipment than I, and was able to chart the pendulum amplitude as it decays, cycle by cycle.
His test results are shown in Figure 7. He compared a 1 mm ball race with 1 mm jewel bearings, both parallel bore and olive shaped holes, with minimum clearance and with .08mm clearance. His results were quite similar to mine, but his objective was not to determine the equivalent coefficients of friction but simply to illustrate that ball races clearly exhibited much less friction. So he did not pursue the physics and the maths to compute the numeric value of µ. I scanned a few of his amplitude plots and loaded them into AutoCAD, picked up the key values and analysed them in my spread sheet. Unfortunately he did not document the starting amplitude in degrees, but used volts dc from his electronic test equipment. If I assume that the results of his testing on an olive jewelled bearing represented a µ of say 0.12, then the µ for his 1 mm ball race comes out at about 0.003 which is similar to my findings in this article. But then he did use a 1 mm race whereas mine are 2 mm ID even though I computed the µ at an effective pivot diameter of 1 mm. I reported my findings in a letter to HJ, November, 2005.
These plots also illustrate the straight line decay which confirms that Coulomb damping is a reasonable assumption for this style of friction testing, even though his half second pendulum was considerably longer than mine.
Dick Stephen’s article may be read in full in HJ, September 2005, or at the BHI web site, article of the month, by following this link:http://www.bhi.co.uk/hj/AoM%20September%2005.pdf
Arbor Shoulder Friction - End Stones
End stones are frequently recommended on high quality clocks to eliminate pivot shoulder friction. It is worth noting that these are totally unnecessary with ball races, since the axial thrust capability provides the same function. But care must be exercised in machining the bearing housing such that there is absolutely no contact between the inner race and the housing. I cannot stress this point too strongly.
Comparison of Friction Results
From these test results it would appear reasonable to assume a µ of 0.003 for the 2 mm ball races, if well soaked out in solvent. For plain pivots and jewelled pivots, a value of 0.15 - 0.18 is representative. This means that the plain pivot has about 60 times as much friction as the ball race. To achieve the same friction in a plain pivot it would have to have a diameter of 0.017 mm or 0.0007”.
It should be noted that this analysis relates only to bearing friction, which is only one portion of the total friction losses in the train. Gear friction and escapement friction are probably much larger.
Lubrication
The type and viscosity of the lubrication in the “as shipped” bearing is highly significant and represents a considerable drag inside the bearing. I initially rinsed out the test bearings with kerosene (paraffin) and acetone or isopropyl alcohol, but I now recommend that the grease or oil be soaked out with white spirit since I have discovered that it dissolves grease and oil much better. I expect that the solvent leaves a thin residue of lubricant, although it is doubtful if this is still there after say twenty years or so. However manufacturers recommend completely dry bearings for absolutely the lowest friction. This is thought to reduce bearing life expectancy somewhat.
My technique is to soak and rinse the bearings in the solvent multiple times, refreshing the solvent each time, draining them on white tissue paper in between. Initially the tissue is stained, but after several repeats, the dried tissue is quite clean, so virtually little additional grease or oil is being extracted, even for shielded bearings. The solvent used should be a hydrocarbon petrochemical variety for best effect in dissolving the grease or oil, and white spirit is a good choice. A friend of mine rotates the bearings in the solvent at fairly high speed to assist in the agitation. This appears to be a good idea.
A good test for a the effectiveness of a rinsing solvent is to place some in say the lid of a jar, then add a single drop of lubricating oil in the middle of it. Try another with methylated spirits for comparison. After 30 minutes the one with white spirits will show how the oil has dissolved and dispersed, while the drop in the meths will still be a contained blob, almost as if it were in water.
Corrosion
There are two types of materials in use in the commonly obtainable bearings.
SAE52100 Chrome Steel as used in the economy pack races and other lower cost races
AIS I 440C Stainless Steel (hardened)
Naturally the chrome steel is cheaper, but possibly may corrode in the long term when the maximum bearing life is desired. I have now switched to using the hardened stainless steel variety. I prefer shielded races to keep out any dust. It is amazing how dust infiltrates a clock movement. I recently took the hood off my longcase clock and noticed a vale of dust on the seat board. And this was only after a couple of years. And the hood fitted very well with barely a 1 mm air gap. Changes in atmospheric pressure probably pumps air in and out, bringing dust with it.
Another type of material in use today is of a ceramic nature for the balls only, or for the entire bearing. However I have not tested these even though they are reported to have very low friction.
Bearing Life and Future Availability
Will such bearings still be available when the present ones need replacing? Firstly, how long are they likely to last before they cause trouble or fail? While it is probably unrealistic to rely on the manufacturer’s standard bearing life formulae with the ultra light loadings and stop-start motion found in our clocks, the calculations do indicate an extremely long life expectancy. For the bearings in my Vienna regulator and the loadings present, the most critical bearing is the one at the end of the centre arbor, and the calculated life is 11,000 years! The great wheel arbor with its larger bearings, comes out at 31,000 years. It is doubtful if this long life would actually be achieved, but it does indicate that very long lives could be expected, and a full strip-down service will be very infrequent. It is my belief that the widespread use of these bearings in delicate instrumentation is increasing, rather than decreasing, so I do not expect availability to be a problem. One only need look at the web site referenced above to see the enormous range of bearings available today. There are some 1,500 individual bearings catalogued in the range from 0.6mm ID to 7mm ID.
Clock Service
This may well be the Achilles Heel of the ball race. When it comes to the future servicing of clocks so fitted, long after the builder of the clock has passed on, will the typical clock repairer know how to perform the task adequately? Teaching clock restorers to understand and respect ball bearings, service them correctly, and to procure replacements, is a different matter altogether. Movements fitted with ball races cannot just be dunked into aggressive cleaning fluid with the expectation that the clock will ever run again! Some repairers seem to live in a world from several centuries ago when ball races had not been developed. Getting adequate servicing in the future may be a major problem. So do leave a clear inscription inside your clock that it has ball races fitted, and perhaps some notes on how to service them! I referenced Sattler Clocks earlier on for their use of ball races, however for the upper arbors they appear to have reverted to jewels apparently because of this service issue, perhaps aggravated by the use of open races. In spite of this, their recent fifty year anniversary clock, Opus Temporis, which is a striking clock, utilizes forty ball races in total.
Even so, if the clock stops and refuses to run, how will the repairer know which bearing is at fault, assuming he can see no other cause. The best way would be to test each bearing in a fiction testing rig similar to Figure 3. A faulty bearing would show up fairly quickly. Then flushing it with white spirit may return it to a good condition, or a replacement procured, and flushed out as discussed earlier. Perhaps he should flush out all of the ball races, but he should NOT add any lubrication!
The question of open races versus shielded races is pertinent. Sattler opted for open races presumably on the grounds that they can be flushed out quite readily, whereas the shielded race requires more effort, unless one is prepared to remove the shields and refit them which is exceedingly risky. The question of dust infiltration into a shielded race in a clock environment is a question I cannot answer at this stage. My experience is limited to only ten years. So far no problems have arisen.
Another cause for a clock with ball races to stop is insufficient washing out of the lubricant in the first place. Lubricant may work its way into the ball track and change the viscous drag. Thorough and complete rinsing cannot be stressed too much. Spinning the races while immersed is probably a good approach.
Robustness
One way of reducing the friction with plain pivots is to reduce the pivot diameter. This leads to very fragile pivots which are more easily snapped off during assembly if the arbor is allowed to tilt too much. The arbor for the 2 mm ball races is massively robust by comparison. However the race that it is going into must be respected since it now becomes the more fragile component in the assembly process. It will tolerate some degree of angular misalignment during assembly, but it should still be respected. Stainless steel then becomes the material of choice for the arbors, since it is not acting as a bearing surface and will resist corrosion and tarnishing.
Cost
Here the ball race initially falls down. It is clearly more expensive. But over the life of the clock it may possibly come out in front due to the reduced service interval and service cost.
In the second part of this article, some thoughts on the fitting of ball races will be presented.
APPENDIX for Part 1
1) Definition of Coefficient of Friction (µ)
µ = Ff / Nr where Ff = the force necessary to cause sliding
Nr = the normal reaction force between the object and the supporting surface
Static µ = Ff/Nr at the point when sliding just commences
Dynamic µ = Ff/Nr when steady sliding movement is established. It is usually less than Static µ

2) Derivation of Equation for Calculating µ from Test Results
The potential energy in the bob (Ep) at the start of the swing is dissipated as friction in the bearing (Ef) as it coasts to a stop. Each swing dissipates a portion of the initial stored energy.
Assuming:
L = Pendulum Length mm
α = Initial amplitude degrees
r = Radius of the bearing pivot (effective) mm – 0.5mm used for 2 mm ID Races
Mg = Force due to bob mass and gravity (this ultimately cancels out)
g = Acceleration due to gravity
N = Total number of pendulum cycles to decay
Ep = Potential energy in bob at start before the pendulum is released
Ef = Total energy dissipated due to bearing friction during decay
Lift = Height of bob relative to bottom of swing mm at start of swing
Di = Initial distance travelled at pivot radius in first full pendulum cycle mm
Davg = Average distance travelled at pivot radius in one full pendulum cycle mm
a) Potential energy of Bob at start - Ep
Ep = Mg * Lift
Lift = L - L* cos(α) = L(1 – cos(α))
Ep = Mg*L(1 – cos(α)) Equation A
b) Energy dissipated by coulomb friction in bearing – straight line decay – Ef
Ef = Number of cycles * average pivot surface distance travelled per cycle * Reaction force * µ
Since the decay is assumed to be linear, the average distance travelled will equal half the first distance of the initial full swing at the radius of the pivot for a full return cycle of the pendulum. Total friction is drag on the surface of the pivot at the effective radius of the pivot.
Di = 2*r*π*(4*α)/360 =2*r*π*α/90
Davg = .5*Di = .5*2*r*π* α/90 = r*π* α/90
Ef = N * Davg * Mg * µ
Ef = N*r*π*(α/90)*Mg* µ Equation B
c) Equate Ep and Ef, equations A & B, then solve for µ
Ef = Ep
N*r*π*(α/90)*Mg*µ = Mg*L(1 – cos(α))
Divide through by N*r*π*(α/90)*Mg and rearrange
μ = 90*L(1- cos(α))/ (N*r*π*α) See equation 1 earlier
Miniature Ball Bearings in Clocks by Rex Swensen - Sydney
Part 2 – Techniques for Fitting Miniature Ball Bearings in Clocks
Fitting Ball Races
The following thoughts are from my own experience, and there may be other approaches that work equally as well. Two important points to observe in these notes are firstly the tightness of the races on the arbors and in the bores, and secondly the need to allow clearance in the housing against the inner race so that absolutely no rubbing can occur.

Great Wheel Bearings
These have been described in many constructional articles. Figure 8 shows a typical layout for a 5mm ID by 11mm OD race mounted in a 3 mm plate. The housing is located in the plate, in an accurately bored hole. It is typically attached with three 10BA screws. On the winding side (shown), the hole for the arbor must have clearance around the arbor. The fit of the race in the housing should be an “easy push fit” – not tight, as it is then difficult to remove. The fit on the arbor should be a very easy push fit, with the normal amount of “shake”. Note the clearance for the inner race in the housing. This is extremely important to minimize friction. Loctite should NOT be used.
If you are fitting ball races to the great wheel arbor, then it is wise to also fit one to the weight pulley.
Other Arbors, including the Pallet Arbor
The arrangement I have used is shown in Figure 9. Here the bearing is sunk directly into the clock plate, in a blind hole. A special spotface cutter was made as shown in Figure 10. It is made from 1/4" silver steel. The four teeth were hand filed, hardened and polished before the spigot was pushed in. The spigot is 3/32" to suite a 3/32" pilot hole. This provides clearance over the 2mm arbor if it happens to projects through. In the machining of this cutter, be sure to provide about 0.005" clearance for the inner race to ensure that the inner race does not rub against the plate. This is highlighted in the detail in Figure 9.
I made my cutter slightly oversize on the 5mm OD, then stoned it down between test cuts to aim for the somewhat elusive "easy push fit". On no account should the bearing be a tight fit, mainly to ensure that it will come out readily. The fit on the arbor may be fairly loose to ensure end float. The teeth were hand filed, indexing by “eye ball”.
It would be better if the cutter flutes were somewhat deeper than shown to aid chip clearance.
You might think a slot drill or end mill would be better, but mine did not cut truly to size, and I wanted to have a pilot spigot to guide the cutter. All the arbor holes were drilled at 3/32" in one setting with both plates clamped together, then opened out from the inside with the spotface cutter to leave a shouldered hole.
Another approach suggested by a friend, is to bore the hole very slightly under size then push in a hardened and polished arbor to burnish the hole to size. Do not use a rotating arbor, just a stationary arbor in the drill press for good alignment. However I have not tried this myself.
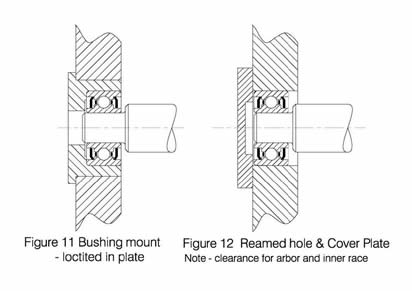
Figures 11 and 12 show several variations for mounting bearings. A plain reamed hole may also be used if flanged bearings are fitted. Here the flange controls the axial positioning of the bearing from the inside.
Miniature bearings MUST be handled with care. The depth of material in the ring groove is tiny and may be damaged with excessive force when fitting, especially angular tilting.
Bearing materials

The preferred material is AIS I 440C Stainless Steel which is a fully hardened stainless steel, but it is usually more expensive. The alternative is SAE 52100 Chrome Steel which is cheaper but open to corrosion in the long term, similar to any un-blued hardened alloy steel.
Procurement Source
All of my bearings were procured from Miniature Bearings Australia via their web site:
http://www.smallparts.com.au/store/partslist/bearingsballsinglerowradialunflanged/ballbearings/all/141/3/ . Look for Bearings, Ball, Single row, Radial, Unflanged. The catalogue is huge, but not all bearings are carried as stock items. Prices vary considerably from time to time so keep an eye on them. Note also, that the minimum freight charge is $A9.35 within Australia, but $A30.00 for International shipments, even if you buy just one tiny bearing. So look ahead and buy up big, or pool your order with others. Similar suppliers are probably located in other parts for the world.
A friend of mine in the UK obtains his bearings from Arc Euro Trade at:
However the range available is not near as large, and the information on each bearing is far less.
Conclusions
The reduction in coefficient of friction, and the assumed reduction in wear and maintenance requirements, makes a very strong case for ball races on all arbors. Many constructors fit them to the great wheel arbor on the basis that it is the more heavily loaded. This is true but it also has the most torque applied. The upper arbors have much less load, but also much less torque. It could be that friction has an equal or greater impact at the top of the train than lower down.
The economy grade races from MBA, at a cost of approximately a dollar each, appear to be quite adequate for clock applications. However corrosion is still an open question, so I have adopted the stainless steel variety for future use.
I have also used them on the pallet arbor which is oscillating about 3 degrees or so. Ball races are generally not recommended for this mode of use, but the loads on this arbor are the lightest of all, so I have confidence that long, trouble free life will be achieved. It has been suggested that they could be used for pendulum pivots as well, even eliminating the crutch, but here the loads are considerable due to bob mass, so personally I would not recommended this approach, particularly for seconds beating pendulums with heavy bobs.
As stated earlier, it would appear reasonable to assume a µ of 0.003 for these tiny races, if well soaked out in solvent. For plain pivots a value of 0.15 - 0.20 is representative. This means that the plain pivot has about 60 times more friction than the ball race. However this will not produce a proportional reduction in drive weight since the predominant friction in the train is dry gear friction which combines sliding and rolling with each pair of wheels and pinions. Minimum friction occurs when the engagement of all pairs are on the line of centres when rolling contact occurs, and maximum when all pairs are just engaging when significant sliding contact occurs. Escapement friction is also a big consumer of energy.
Final Thought
It is interesting to note again that a 2 mm ID ball race with a µ of 0.003, has an equivalent frictional drag to a plain pivot with a diameter of 0.017mm (0.0007”)! Much less than a human hair! A ball race has only 1/60th the friction of a plain pivot even if it is jewelled!
